Комплексный анализ I/Билеты/Основные элементарные функции

Определение. ${\textstyle \sqsupset D\subset {\overline {\mathbb {C} }}}$– область, ${\textstyle f:D\rightarrow \mathbb {C} }$называется однолистной в ${\textstyle {\text{D}}}$,если ${\textstyle \forall Z_{1},Z_{2}\in D\quad f\left(z_{1}\right)=f\left(z_{2}\right)\Leftrightarrow z_{1}=z_{2}}$.

Определение. Область ${\textstyle D\subset {\overline {\mathbb {C} }}}$ называется максимальной областью однолистности для ${\textstyle f}$, если:

1. ${\textstyle f}$ определена в ${\textstyle D}$ и однолистна в ней;
2. ${\textstyle \not \exists D^{\prime }\supset D:f}$ определена на ${\textstyle D'}$ и однолистна в ней.

Основные элементарные функции

Степенная функция

${\textstyle {\begin{array}{l}{z^{n},n\in N}\\{z=r(\cos \varphi +i\sin \varphi )}\\{z^{n}=r^{n}(\cos n\varphi +i\sin n\varphi )}\\{z^{n}:\mathbb {C} \rightarrow \mathbb {C} }\end{array}}}$

${\textstyle z_{1}^{n}=z_{2}^{n}\Leftrightarrow \left\{{\begin{array}{c}{\left|z_{1}\right|=\left|z_{2}\right|}\\{n\arg z_{1}\equiv n\arg z_{2}(\mod 2\pi )}\end{array}}\right.\Leftrightarrow \left\{{\begin{aligned}\left|z_{1}\right|=\left|z_{2}\right|&(1)\\\arg z_{1}-\arg z_{2}={\frac {2\pi k}{n}},k\in Z&(2)\end{aligned}}\right.}$

${\textstyle D}$ максимальная область однолистности для ${\textstyle z^{n}\Longleftrightarrow \not \exists z_{1},z_{2}\in D:}$ выполняются (1) и (2).

Пример.

Корень n-ой степени

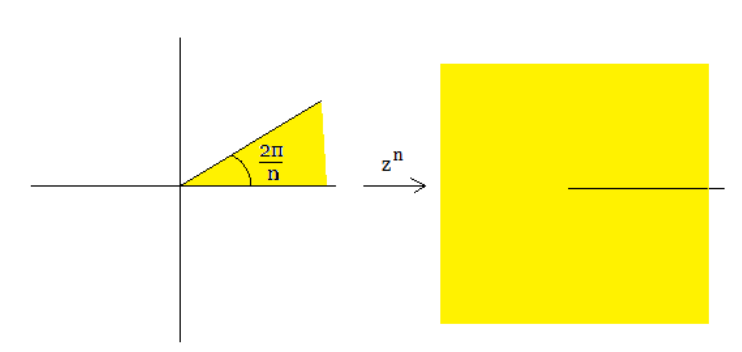
${\textstyle {\sqrt[{n}]{z}}={\sqrt[{n}]{r}}\left(\cos {\frac {\operatorname {Arg} z}{n}}+i\sin {\frac {\operatorname {Arg} z}{n}}\right)}$ – ${\textstyle n}$-значная функция.

${\textstyle {\sqrt[{n}]{z}}=w\Rightarrow z=w^{n}\Longrightarrow |z|(\cos \varphi +i\sin \varphi )=|w|^{n}(\cos(n\arg w)+i\sin(n\arg w))}$

Определение. ${\textstyle \sqsupset D}$ область, ${\textstyle F:D\rightarrow \mathbb {C} ^{n\;(or\;\infty )}}$; функция ${\textstyle f}$ называется ветвью ${\textstyle F}$,если ${\textstyle \forall z\in Df(z)\in F(z)}$.

Примечание. Не всегда можно выделить непрерывную ветвь.

Пример. У ${\textstyle {\sqrt {Z}}}$ не существует непрерывной ветви в ${\textstyle \mathbb {C} }$.

Функция Жуковского

${\textstyle \mathrm {J} (z)={\frac {1}{2}}\left(z+{\frac {1}{z}}\right):{\overline {\mathbb {C} }}\rightarrow {\overline {\mathbb {C} }}}$

${\textstyle {\begin{array}{l}{\mathrm {J} (\infty )=\infty }\\{\mathrm {J} (0)=\infty }\end{array}}}$

${\textstyle J\left(z_{1}\right)=J\left(z_{2}\right)\Leftrightarrow z_{1}z_{2}=1\quad (\infty *0=1)}$

${\textstyle D}$ является областью однолистности ${\textstyle \Leftrightarrow \not z_{1},z_{2}\in D:z_{1}z_{2}=1}$.

Таким образом, максимальными областями однолистности являются внутренность единичной окружности и её внешность, причём переходят они под действием функции Жуковского в одно и то же множество. Так, для любой точки ${\textstyle a}$ внутри единичной окружности есть точка ${\textstyle {\frac {1}{a}}}$ вне этой окружности,а ${\textstyle \mathrm {J} (a)=\mathrm {J} \left({\frac {1}{a}}\right)={\frac {1}{2}}\left(a+{\frac {1}{a}}\right)}$. Выясним,что это за область, например, выясним, во что перейдёт внутренность единичной окружности ${\textstyle |r|<1}$:

${\textstyle \mathrm {J} (z)=J(r(\cos \varphi +i\sin \varphi ))={\frac {1}{2}}\left(r(\cos \varphi +i\sin \varphi )+{\frac {1}{r}}(\cos \varphi -i\sin \varphi )\right)=}$

${\textstyle ={\frac {1}{2}}\left(r+{\frac {1}{r}}\right)\cos \varphi +i{\frac {1}{2}}\left(r-{\frac {1}{r}}\right)\sin \varphi }$

Эти точки при фиксированном ${\textstyle r}$ и изменении ${\textstyle \varphi }$ образуют эллипс с полуосями:

${\textstyle {\begin{array}{c}{a={\frac {1}{2}}\left(r+{\frac {1}{r}}\right)\quad \mathrm {H} \quad b={\frac {1}{2}}\left({\frac {1}{r}}-r\right)}\\{a^{2}-b^{2}=1}\end{array}}}$

При приближении ${\textstyle r}$ к нулю ${\textstyle a}$ стремится к бесконечности, следовательно, так как ${\textstyle a^{2}-b^{2}=1}$, ${\textstyle b}$ тоже стремится к бесконечности, то есть получаются расширяющиеся эллипсы,а при приближении ${\textstyle r}$ к единице ${\textstyle b}$ стремится к нулю, то есть в пределе получается эллипс с полуосями 1 и 0, то есть отрезок ${\textstyle [-1,1]}$; в итоге получается, что функция Жуковского переводит внутренность единичной окружности и её внешность во всю плоскость, кроме отрезка ${\textstyle [-1,1]}$.

Функция, обратная функции Жуковского

${\textstyle \mathrm {J} ^{-1}(z)=z+{\sqrt {z^{2}-1}}}$ двузначная функция.

${\textstyle {\begin{array}{c}{{\frac {1}{2}}\left(w+{\frac {1}{w}}\right)=z}\\{w^{2}-2wz+1=0}\\{w=z+{\sqrt {z^{2}-1}}}\end{array}}}$

Пример. Область, в которой у функции, обратной функции Жуковского, выделяется непрерывная ветвь: ${\textstyle D=\mathbb {C} \backslash [-1,1]}$.

Одна ветвь переводит эту область обратно во внутренность единичной окружности,а другая во внешность единичной окружности.

Экспонента

${\textstyle {\begin{array}{c}{z=x+iy}\\{e^{z}:=e^{x}(\cos y+i\sin y):\mathbb {C} \rightarrow \mathbb {C} \backslash \{0\}}\end{array}}}$

Поищем области однолистности для экспоненты:

${\textstyle e^{z_{1}}=e^{z_{2}}\Leftrightarrow \left\{{\begin{array}{l}{e^{x_{1}}=e^{x_{2}}\Leftrightarrow x_{1}=x_{2}}\\{y_{1}-y_{2}=2\pi n,n\in Z}\end{array}}\right.}$

Следовательно, ${\textstyle D}$ область однолистности для ${\textstyle e^{z}\Leftrightarrow \exists z_{1},z_{2}\in D:z_{1}-z_{2}=2\pi ni}$, то есть примером максимальной области однолистности может быть любая горизонтальная бесконечная полоса высотой ${\textstyle 2\pi }$, и экспонента переводит её во всю плоскость без положительного луча действительной прямой. Докажем это, рассмотрев какой-нибудь вертикальный отрезок, входящий в нашу полосу. Пусть это будет отрезок от точки ${\textstyle \left(x_{0},y_{0}\right)}$ до точки ${\textstyle \left(x_{0},y_{0}+2\pi \right)}$. Экспонента переведёт его в кривую, задаваемую формулой ${\textstyle e^{x_{0}}(\cos y+i\sin y)}$,где ${\textstyle y\in \left(y_{0},y_{0}+2\pi \right)}$, а это есть окружность с выколотой правой точкой радиуса ${\textstyle e^{x_{0}}}$. Так как ${\textstyle x_{0}}$ можно выбрать от ${\textstyle -\infty }$ до ${\textstyle +\infty }$, то этот радиус может меняться в пределах ${\textstyle (0,+\infty )}$, то есть эти окружности с выколотыми точками заполнят всю плоскость, кроме положительного луча действительной оси. Заметим, что из определения видно, что экспонента ${\textstyle 2\pi i}$-периодична.

Логарифм

${\textstyle \operatorname {Ln} z=\ln |z|+i\operatorname {Arg} z}$ бесконечнозначная функция (в данном случае счётнозначная)

${\textstyle {\begin{array}{c}{e^{w}=z}\\{e^{Rew}(\cos(\operatorname {Im} w)+i\sin(\operatorname {Im} w))=|z|(\cos(\operatorname {Im} z)+\sin(\operatorname {Im} z))}\\{\operatorname {Re} w=\ln |z|}\\{\operatorname {Im} z=\operatorname {Arg} z}\end{array}}}$

Пример. Область,в которой выделяется непрерывная ветвь:

${\textstyle {\begin{array}{c}{\mathbb {C} \backslash [0,+\infty )}\\{\ln |z|+i\arg z\in \operatorname {Ln} z}\end{array}}}$

Тригонометрические функции

${\textstyle {\begin{aligned}\sin z&:={\frac {e^{iz}-e^{-iz}}{2i}}\\\cos z&:={\frac {e^{iz}+e^{-iz}}{2}}\end{aligned}}}$

Все тригонометрические формулы остаются верными. Вспомним гиперболические функции:

${\textstyle {\begin{aligned}\operatorname {ch} z&:={\frac {e^{z}+e^{-z}}{2}}\\\operatorname {sh} z&:={\frac {e^{z}-e^{-z}}{2}}\end{aligned}}}$

Видно, что гиперболические и тригонометрические функции связаны так:

${\textstyle {\begin{aligned}\cos z&=\operatorname {ch} iz\\\sin z&={\frac {\operatorname {sh} iz}{i}}\end{aligned}}}$

${\textstyle \sin z={\frac {e^{iz}-e^{-iz}}{2i}}={\frac {1}{2}}\left({\frac {e^{iz}}{i}}+{\frac {i}{e^{iz}}}\right)=J\left({\frac {e^{iz}}{i}}\right)}$

${\textstyle \sin z_{1}=\sin z_{2}\Leftrightarrow \left[{\begin{array}{c}{e^{iz_{1}}=e^{iZ_{2}}}\\{{\frac {e^{iz_{1}}}{i}}*{\frac {e^{iz_{2}}}{i}}=1}\end{array}}\right.\Leftrightarrow \left[{\begin{array}{c}{iz_{1}=iz_{2}+2\pi ki,k\in Z}\\{e^{i\left(z_{1}+z_{2}\right)}=-1}\end{array}}\right.\Leftrightarrow }$

${\textstyle \Leftrightarrow \left[{\begin{array}{c}{z_{1}-z_{2}=2\pi k,k\in Z}\\{i\left(z_{1}+z_{2}\right)=\operatorname {Ln} (-1)=i(\pi +2\pi n),n\in Z}\end{array}}\right.\Leftrightarrow \left[{\begin{array}{l}{z_{1}-z_{2}=2\pi k,\quad k\in Z\quad (1)}\\{z_{1}+z_{2}=\pi +2\pi n,\quad n\in Z\quad (2)}\end{array}}\right.}$

Получается, область ${\textstyle D}$ будет максимальной областью однолистности тогда и только тогда, когда ${\textstyle \not \exists Z_{1},Z_{2}\in D}$, что для них выполнены условия 1 и 2.

Пример максимальной области однолистности:

Посмотрим,во что её переводит синус:

Докажем правильность последнего перехода. Известно,что единичный круг переходит во всю плоскость без отрезка ${\textstyle [-1,1]}$. Осталось понять, куда переходит отрезок ${\textstyle [0,i]}$:

${\textstyle J(iy)={\frac {1}{2}}\left(iy+{\frac {1}{iy}}\right)={\frac {i}{2}}\left(y-{\frac {1}{y}}\right),{\text{ где }}0\leq y\leq 1}$

При этом ${\textstyle {\frac {1}{2}}\left(y-{\frac {1}{y}}\right)}$ меняется в пределах ${\textstyle (-\infty ,0]}$, значит, ${\textstyle J(iy)}$ меняется в пределах ${\textstyle (-\infty ,0]}$ по нижней мнимой полуоси, что и требовалось доказать.